2022英语周报高一新课程40答案

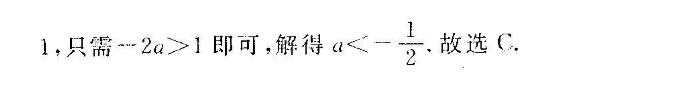
11.C【解析】根据题意,得f(x)=e 2ax 2a,若f(x)有最小值,即f(x)在(0,十∞)上先递减再递增,即∫"(x)在(0, ∞)先小于0,再大于0,令∫(x)<0,得e<-2a(x 1),令g(x)=e,h(x)=-2a(x 1),只需直线h(x)的斜率-2a大于过(1,0)的g(x)的切线的斜率即可,设切点为(xn,u),则切线方程为y-eo=e(x-x,),将(-1,0)代入切线方程得x0=0,故切点为(0,1),切线的斜率为1,只需2a>1即可,解得a<-1故选(.

21.解:(1)由题意,可得S△MN=2OAMN=p×2p22,解得p=3,故抛物线C的标准方程为y2=6x(4分)(2)设M(x1,y1),N(x2,x2),直线MN的方程为x=my a,.my"ta联立得y2-6my-6a=0,△=36m2 24a>0y: y2=6m,yy2=-6a,由对称性,不妨设m>0(7分)(1)当a<0时,∵y1y2=-6a>0,y,y2同号,又AAN m21y2所以t2=136n2y1 y不论a取何值,t与m有关,即a<0时,A不是“稳定点”;(10分)()当a>0时,6a<0∵.y1,y2异号LAMANI 千所以t2(y1y2)(y1 y2)2-4yI y2136m2 24a1 m21- 36a1 .3a-1所以当且仅当时,t与m无关此时A为抛物线C的焦点,即抛物线C的对称轴上仅有焦点这一个“稳定点”(12分)

以上就是2022英语周报高一新课程40答案，更多英语周报答案请关注本网站。