2022高二英语周报29期答案

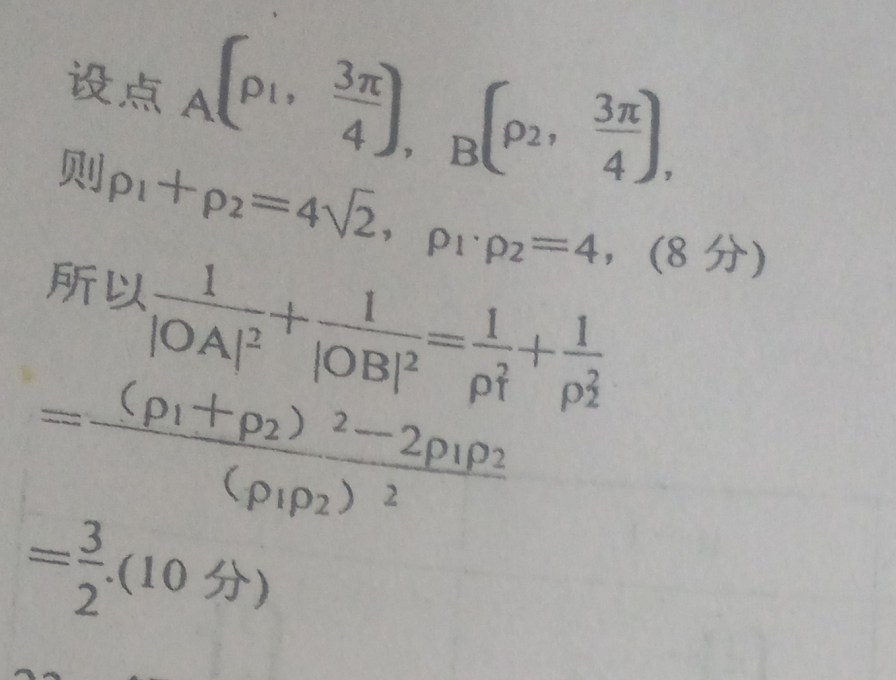
设点A(23丌4P2,则B4J,p1 p2=4、2,pp2=4,(8分)所以1 =1 1IOAI OB12 pf p2p1 p2)2-2p1p2pp2)232(10分)3 v6cose22.解:(1)由曲线C的参数方程为参数)消参得曲线C的普通方程y=l visine为(x 3)2 (y-1)2=6.(2分)由psin0得psin pcos=0所以直线1的直角坐标方程为x y=0.(4分)(Ⅱ)将x=pcos,y=psin代入曲线C:(x 32 (-1)2=6得p2 (6c0-2sin0)p 4=0,(5分)由psin pcos=0得=(p∈R).(6分)将=5(p∈R)代入p2 (6c0s-2sine)p 4=0,得p2-42p 4=0

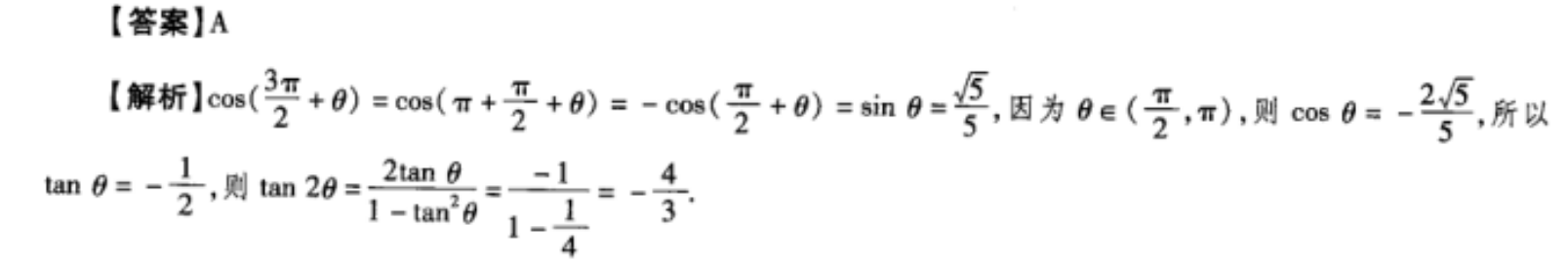
【答案】A【解析】(2 0)=(m 6)=-cm( 0)=m=因为6∈(,m),则cos025,所以tan 8=,则tan26tan 8tan 613

以上就是2022高二英语周报29期答案，更多英语周报答案请关注本网站。