2022高一英语周报59期答案

2.解:(1)令F(x)=x 2=x2 2,则F(x)=21分令F(1,得x=13分因为F(1)=3,所以切线l的方程为y=x 分(2)A G()=2f(r) ag(r)=2efl-(a 2)xtaln rta则G(x)=2 2e1-(a 2)=(a 2)x当x≥1时,f(x)=e-1-1≥0,故f(x)在[1, ∞)上单调递增所以f(x)≥f(1)=0,即e≥x,2x2-(a 2)x a(2x-a)(x-1)所以G(x)≥①当a≤2时,G(x)≥0在[1, ∞)上恒成立,即G(x)在[1, ∞)上单调递增因为G(x)≥G(1)=0,所以a≤2满足题意8分②当a>2时,令H(x)=G(x)=a 2c-1-(a 2),则H(x)=- 2c1,因为H(x)在[1, ∞)上单调递增且H(1)=2-a<0,H(G)=2e-1-1>0所以H(x)在(1,a)上存在唯一的零点x0当x∈[1,xo)时,H(即H(x)在(1,x0)上单调递减,此时H(x)≤H(1)=0,则G(x)在(1,x)上单调递减,此时G(x)

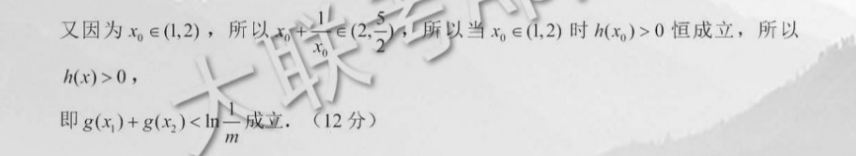
22.【解析】(1)由题意,f(x)=-mhn4,故/()m x,(1分)又x>2,故当m20时,f()0,时国数f(5在(这 x)上单调递减:(2分)当m<0时,令f(x)=0,m,故x√=m若sm≤0时,f(x)<0,此时函数f(x)在(2, )上单调递减:(3分)若√-m>2,即m<-4时,当x∈(2,y-m)时,f(x)>0,当x∈(√-m, ∞x)时,f(x)<0,此时函数f(x)在(2,-m)上单调递增,在(-m, ∞)上单调递减.(4分)综上,m≥-4时,函数f(x)在(2, ∞)上单调递减:当m<-4时,函数f(x)在(2,√-m)上单调递增,在(=m, )上单调递减.)(5分(2)由题意A 23x2mmx 23x=x2-4,为g有两个极值点x,x2,所以g(x)=0有两个正根x1,x,A=12-4m>0则{x x2=23>0,解得m∈(03),(7分)x,x,=m>0所以g(x) g(x2)=23(x x2)-mmx)-(x2 x2)-8=-mm m-2,所以要证g(x) g(x) 0,(8分)构造函数M(x)=xmx-x-x 2,则h(x)=hx-1,易知h()在0.3)上为增函数,且h(1)=-1<0,h(2)=hn2-->0,所以存在x∈(1,2),使h(x)=0,(9分)即mx=,且当x∈(.x)时,Mx)<0,Mx)单调递减:当xe(x,2)时,(x)>0,h(x)单调递增所以x)在(.2)上有最小值为h(x)=x如一下如x中23=(x ),(10分又因为x∈(2),所以(2.)所以当x∈(,2)时h(x)>0恒成立,所以h(x)>0,即g(x) g(x2) <一成立.(12分)< p>

以上就是2022高一英语周报59期答案，更多英语周报答案请关注本网站。