

21,(1)证明:当a=1时,f(x)=e-x-x2,所以f"(x)=e2-2x-1令g(x)=e-2x-1则g'(x)=e-2.令g'(x)=0,即e-2=0,解得x=ln当x∈(-∞,ln2)时,g'(x)<0,g(x)单调递减当x∈(hn2, ∞)时,g'(x)>0,g(x)单调递增所以g(x)m=g(ln2)=1-2ln2<0.(2分)又因为0∈(-∞,hn2).且g(0)=0所以当x∈(0)时,g(x)>0,即f(x)>0,∫(x)单调递增当x∈(0,ln2)时,g(x)<0,即f(x)<0,f(x)单调递减;所以x=0是函数f(x)的一个极大值点(4分)又g(2)=e2-5>0,所以存在x∈(hn2,2),使g(x)=co-2x-1=0,所以当x∈(0,x。)时,g(x)<0,f'(x)<0,f(x)单调递减;当x∈(x0, ∞)时,g(x)>0,f(x)>0,f(x)单调递增.所以x=x。是f(x)的一个极小值点综上所述,函数f(x)有两个极值点(6分)(2)解:不等式f(x)≥x-x2 b(b∈R)恒成立等价于e一(a 1)x-b≥0恒成立,令h(x)=e-(a 1)x-b,则h'(x)=e-(a 1)①当a 1≤0时,h(x)>0,h(x)在区间(-∞,十∞)上单调递增且h(0)=1-b与h(x)≥0恒成立矛盾,故a 1≤0不符合题意;(7分)②当a 1>0时,令h'(x)=0,解得x=ln(a 当x∈(-∞,ln(a 1)时,h'(x)<0,h(x)单调递减;当x∈(ln(a 1), ∞)时,h'(x)>0,h(x)单调递增所以当x=ln(a 1)时,h(x)mn=(a 1)-(a 1)ln(a 1)-b(8分)则(a 1)-(a 1)ln(a 1)-b≥0恒成立即(a 1)b≤(a 1)2-(a 1)2ln(a 1).(9分)令x'In x(r>0)所以g'(x)=x(1-2nx),令g'(x)=0,解得x=√e,当x∈(0,e)时,g'(x)>0,g(x)单调递增;当x∈(√e, ∞)时,g'(x)<)单调递减所以g(x)的最大值为g(e)=e,当且仅当a=√C-1,b=时取等号所以(a 1)b的最大值为(12分)

B. CDAD

以上就是2022 英语周报 七年级 GDY 0答案,更多英语周报答案请关注本网站。

 相关文章
相关文章

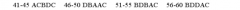
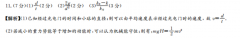
 栏目最新
栏目最新

 随机推荐
随机推荐 热门标签
热门标签