英语周报四川版2021-2022答案

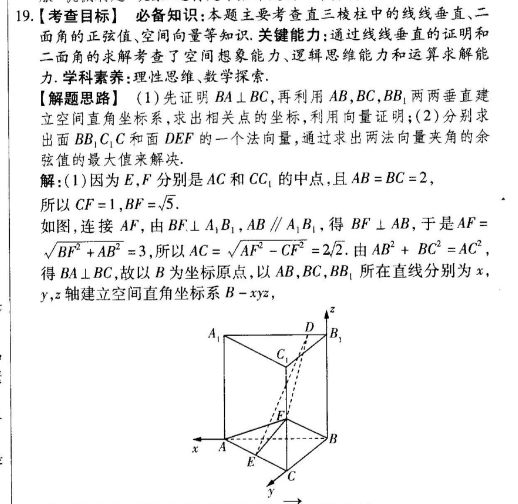
19.【考查目标】必备知识:本题主要考查直三棱柱中的线线垂直、二面角的正弦值、空间向量等知识.关键能力:通过线线垂直的证明和二面角的求解考查了空间想象能力、逻辑思维能力和运算求解能力学科素养:理性思维、数学探索【解题思路】(1)先证明BA⊥BC,再利用AB,BC,BB1两两垂直建立空间直角坐标系,求出相关点的坐标,利用向量证明;(2)分别求出面BB1C1C和面DEF的一个法向量,通过求出两法向量夹角的余弦值的最大值来解决解:(1)因为E,F分别是AC和C1的中点,且AB=BC=2所以CF=1,BF=√5.如图,连接AF,由BF⊥A1B1,AB∥AB,得BF⊥AB,于是AF=BF ABF=3,所以AC=√AF-CF=2.由AB2 BC2=AC2,得BA⊥BC,故以B为坐标原点,以AB,BC,B1所在直线分别为x,y,z轴建立空间直角坐标系B-xy则B(0,0,0),E(1,1,0),F(0,2,1),BF=(0,2,1)设B1D=m(0≤m≤2),则D(m,0,2),于是DE=(1-m,1,-2)所以B.DE=0,所以BF⊥DE(2)易知面BB1C1C的一个法向量为n1=(1,0,0)设面DFE的法向量为n2=(x,y,2),n,又靂=(1-m,1,-2),E=(-1,1,1)所以(1-m)x y-2z=0-x y z=0,令x=3,得y=m 1,z=2-m,于是,面DFE的一个法向量为n2=(3,m 1,2-m),所以cos(n1,n2〉=)2设面BCC与面DFE所成的二面角为6,则in6=√1-m(n1,m2),故当m=时,面BBCC与面DFE所成的二面角的正弦值最小为,即当B1D=时,面BB1C1C与面DFE所成的二面角的正弦值最小.【解題关键】本题求解关键是建立恰当的空间直角坐标系,确定相关点的坐标,再利用空间向量进行运算

【语篇导读】本文是新闻报道。在新冠肺炎流行期间,很多居家的人们想起了为了躲避纳粹迫害而到处躲藏的安妮·弗兰克,安妮在日记中表现出的坚强引导人们如何去正确看待居家躲避病毒。28.B【解析】细节理解题。根据第二段中的 The anneFrank Project . is working to feed and fund students inneed可知,安妮·弗兰克项目旨在帮助有困难的学生,为他们提供食物和资金。故选B。29.A【解析】推理判断题。根据第二段中的 Whileare not hiding from the Nazis, we are indeed hidingrom an oppressiveⅵinus.可知,人们在新冠肺炎爆发而居家期间想到安妮是因为他们都要躲着不能外出,一个是躲避纳粹,个是躲避病毒。故选A30C【解析】推理判断题。根据第三段中的whatAnne has offered for decades is an example of npt justtragedy(悲剧), but also strength, kindness and, grace可知,Gsar认为安妮在躲避纳粹期间表现得非常坚强。故选C。31.D,【解析】细节理解题。根据第四段内容可知,Ruth franklin建议人们在与疫情斗争的困难时期记录下自己生活的点滴。故选D。

以上就是英语周报四川版2021-2022答案，更多英语周报答案请关注本网站。