

1C【解析】设椭圆的左焦点为F,P为短轴的上端点,连接AF,BF,如下图所示:由椭圆的对称性可知,A,B关于原点对称,则|OA=|OB|.又|OF=|OF|,∴四边形AFBF为平行四边形,|AF|=|BF.又|AF| BF|=|BF |BF|=2a=6,解得a=3,又点P到直线l距离d=1-3≥6,解得b≥2,即√a=cx=√9-c≥2,0<∈≤5,e=∈Q·故选C



9.解:(1)由题得,f(x)=2x-2a 2x2-2ax 1令y=2x2-2ax当△=4a2-8≤0,即-√≤a≤时,y≥0,此时f(x)在(0, ∞)上单调递增;当a <一√时,2x2-2ax 1=0有两个负根,此时f(x)在(0,十∞)上单调递增;当a> √2时,2x2-2ax 1=0有两个正根,解得x=或此时f(x)在上单调递增,在a √a-2上单调递减综上,当a≤√2时,函数f(x)在(0, ∞)上单调递增当a>√2时,函数f(x)在( =2十∞)上单调递增,在上单调递减(5分)(2)由(1)可得,x当=,-=x 21=0,x1·n=2,>②,20n1=2x 12ax2=2x2 1a>√2,则>2n∈(0.2),x∈(, ∞). f(x2)-2f(r)=.xi-2axz In r2-2(r-2arr in xi)=-x2 2x In xz-2ln xi 1 2(2) mx=21n2 1- 2 2hnx2 1 2ln2.令t=x2,则1ul g(t)=-t atoN t 1 2ln 2则g(t)=-1- 2t2 3t-124(2t-1)(t-1)2t2

以上就是2022 英语周报 高二 新课程 1答案,更多英语周报答案请关注本网站。

 相关文章
相关文章


 栏目最新
栏目最新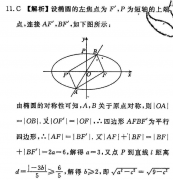



 随机推荐
随机推荐 热门标签
热门标签