
1.【解析】如图所示,因为圆E(x-a) =所以AE=R=,又因为△ABO为等边三角形,所以31an30°-E.得OE=3-1,所以2=1,即p=2,所3以抛物线M:y2=4x,所以C(1,2),F(1,0),作点C关于准线l的对称点C1,则C1(-3,2),所以|PF|PC|=|PF| |PC1|≥|C1F|=√16 4=25.故选B.


2解:(1)由题意得x2 y2=(cosa √3ina)2 (sina√3cosa)2化简得x2 y2=4即曲线C的普通方程为x2 y2=43分直线的极坐标方程展开为2∞0s0-2psn=2,故直线l的直角坐标方程为3x-y-4=0.(5分)(2)显然点P的坐标为(0,-4),不妨设过点P的直=Icos线的参数方程为(t为参数)4 tsin B代入x2 y2=4,得t2-8sin 12=0,△>0(8分设A,B两点对应的参数分别为1,t2,则|PA|·|PB|=|t1t2|=12,即|PA|·|PB|为定值(10分)

以上就是2019到2022英语 周报第19期答案,更多英语周报答案请关注本网站。

 相关文章
相关文章



 栏目最新
栏目最新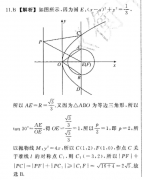

 随机推荐
随机推荐 热门标签
热门标签