2022高三英语周报hz第37期答案

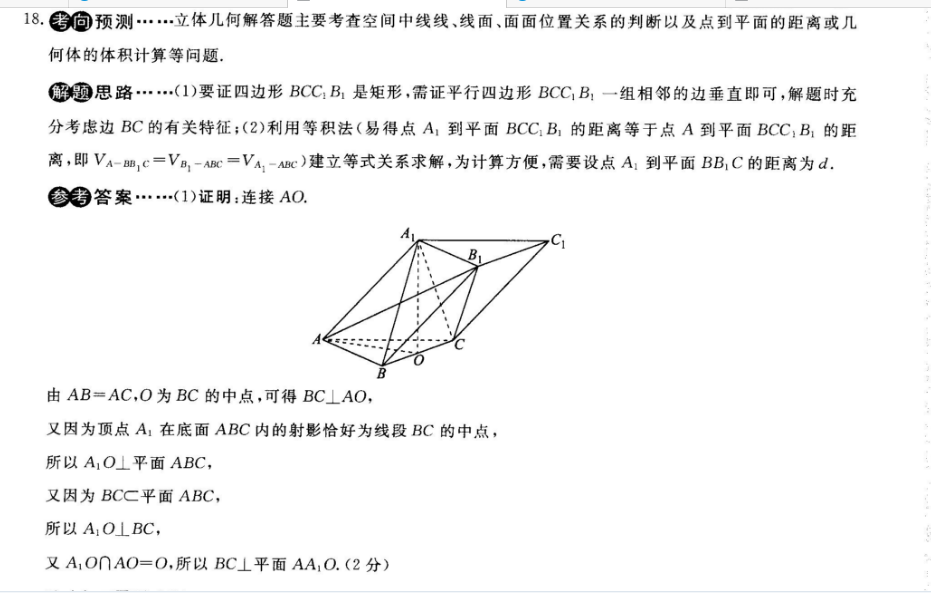
18考向预测……立体几何解答题主要考查空间中线线线面、面面位置关系的判断以及点到平面的距离或几何体的体积计算等问题思路……(1)要证四边形BCC1B1是矩形,需证平行四边形BCC1B1一组相邻的边垂直即可,解题时充分考虑边BC的有关特征;(2)利用等积法(易得点A1到平面BCCB1的距离等于点A到平面BCCB1的距离,即VA-B1c=VB1-AB=VA1-AC)建立等式关系求解,为计算方便,需要设点A1到平面BB1C的距离为d参考答案……(1)证明:连接AO由AB=AC,O为BC的中点,可得BC⊥AO又因为顶点A1在底面ABC内的射影恰好为线段BC的中点,所以A1O⊥平面ABC,又因为BCC平面ABC,所以A1O⊥BC,又A1OnAO=O,所以BC⊥平面AA1O.(2分)又A1O∩AO=0,所以BC⊥平面AA1O.(2分)又AA1C平面AOA1,所以BC⊥AA由BB1∥AA1,得BC⊥BB1,(4分)又四边形BCC1B1是平行四边形,所以四边形BCC1B1是矩形.(5分)(2)连接B1C.由AA1∥BB1,AA1￠平面BCC1B1,BB1C平面BCC1B1所以AA1∥平面BCC1B所以点A1到平面BCC1B1的距离等于点A到平面BCC1B1的距离,即VA-B1CABCA-ABC·(7分)设点A到平面BC的距离为则号×号Sumn:=m,O1d=23,(0分易求得OA=√AB2一BO2=3,OA1=√AAH-AO=√3,S矩形BC1B1BCXBB1=BC×AA1=2√6,(10分)△ABCBCXOA=×2×√3=√3,(11分/6所以d=2√6,即点A1到平面BCGB1的距离为2.(12分)

21.解:(1)由题意可知,命题p为真命题由集合M={xkx2-2kx 1=0,∈R}为空集,得方程kx2-2kx*-1=0没有实数解,所以当k=0时,方程变为1=0,故无解,符合题意当k≠0时,Δ-4k2-4k<0,即0 0的解集为R得Δ=(k…1)2-16<0,解得一3

以上就是2022高三英语周报hz第37期答案，更多英语周报答案请关注本网站。