2018-2022 英语周报 高二 HZ 33答案

20.【命题意图】本题考查利用导数研究函数的单调性、证明不等式,考查分类讨论思想、转化与化归思想,体现了逻辑推理、数学运算等核心素养(1)【解】∵f(x)= xf(x)=esne -are(a e2)(1-x)(1分)当a≥0时,a e>0,由(x)=0,得x=1当x∈(-∞,1)时,f(x)>0;当x∈(1, ∞)时,f(x)<0∴f(x)在(-∞,1)上单调递增,在(1, ∞)上单调递减(2分)当a<0时,由∫(x)=0,解得x=1或x=lhn(-a)(3分)若a=-e,则ln(-a)=1,可得当x∈(-∞,1)时,f(x)<0,当x∈(1, ∞)时,∫"(x)<0f(x)在R上单调递减;(4分)若a<-e,则ln(-a)>1,可得当x∈(-∞,1)时,f(x)<0,当x∈(1,In(-a))时,f(x)>0,当x∈(ln(-a), ∞)时,f(x)<0f(x)在(-∞,1)上单调递减,在(1,hn(-a))上单调递增,在(hn(-a), ∞)上单调递减;(5分)若-e 0,当x∈(1, ∞)时,f(x)<0,∴f(x)在(-∞,hn(-a))上单调递减,在(hn(-a1)上单调递增,在(1, ∞)上单调递减.(6分)(2)【证明】∵a=1,∴要证g(x)≥f(x)在(-∞,1)上恒成立,即证一1-2≥2 x-x2在(-∞,1)上恒成立,亦即证-2x≥x x-1x2在(-,)上恒成立(7分)设F(x)=-211 -x,x∈x则证xF(x)≥0在(-∞,1)上恒成立即可(8分)易得F(x)=(x-1)2 e∴当x∈(-∞,1)时,F(x)>0恒成立,∴F(x)在(-∞,1)上单调递增当x=0时,F(x)=0;当0 0;当x<0时,F(x)<0(10分)∴当x∈(-∞,1)时,xF(x)≥0恒成立即g(x)≥f(x)在(-∞,1)上恒成立.(12分)s名师评本题第(1)问主要考查含有字母参数的分类讨论问题,这是高考对导数内容考查的重点和热点问题,也是考查学生思考和表达数学问题的重要载体,问题常考常新.学生对分类讨论的分类标准往往把握不好,分类讨论比较“乱”,思维缺少条理性.第(2)问考查不等式的证明,也是高考的重点和热点问题.不等式证明的方法更加灵活多样,思维空间更加广阔,对式子变形能力有较高要求,第(2)间,还考查了构造法,要注意定义域,这是学生容易忽视的地方

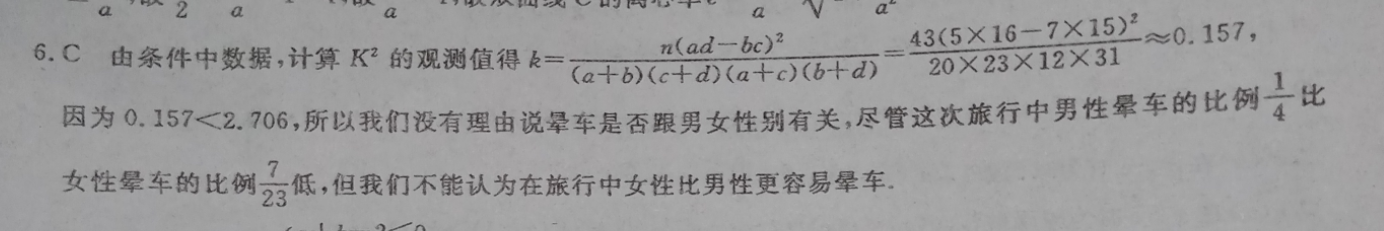
43(5×16-7×15)6.C由条件中数据,计算K2的观测信倡(0(a b)(c d)(a c)(b d)20×23×12×31≈0.157,n(ad-bc因为0.157<2.706,所以我们没有理由说晕车是否跟男女性别有关,尽管这次旅行中男性晕车的比例比女性晕车的比例。低,但我们不能认为在旅行中女性比男性更容易晕车

以上就是2018-2022 英语周报 高二 HZ 33答案，更多英语周报答案请关注本网站。