2022英语周报八年级外研社答案

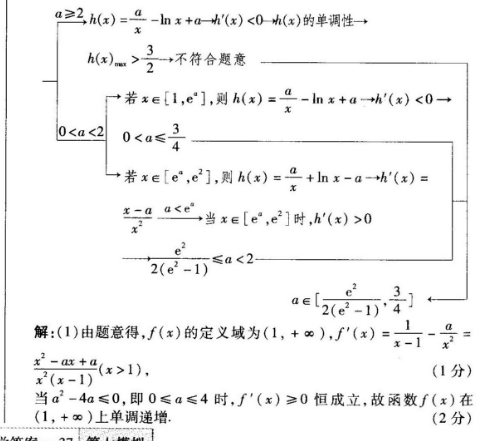
22.【必备知识】本题考查的知识是“了解函数的单调性与导数的关系;能利用导数研究函数的单调性,会求函数的单调区间(其中多项式函数不超过三次)”,“会求闭区间上函数的最大值、最小值(其中多项式函数不超过三次)【关键能力】本题考查运算求解能力、逻辑思维能力【解题思路】(1)/(x)→(x)对分情况计论,r(x)的符号→函数f(x)的单调性(2)当a>0,x∈[1,e]时,f(x 1)- 21≤3-恒成立→当a>0,x∈[l,e2]时,a lhnx-al≤3恒成立构造函数设h(x)= lnx-al(a>0,x∈l,e2(x)=a-lmx a1(x)<0()的单调性→h(x)=> 不符合题意若x∈[1,e],则h(x)=-hnx a→ h(x)<0→0 0≤a 1)(1分)当a2-4a≤0,即0≤a≤4时,f'(x)≥0恒成立,故函数f(x)在(1, ∞)上单调递增(2分)当a2-4a>0,即a<0或a>4时,由f’(x)=-a aA2 A0(x>1),得x1=a √a2-4a若a<0,则x1 0,所以f(x)在(1, ∞)上单调递增;(4分)若a>4,则x2>x1>1,当x∈(1,x1)U(x2, ∞)时,f'(x)>0,当x∈(x,2)时,∫(x)<0,所以(x)在(1,-2 =)上单调递增,在(4-Y0-4n,g √0-4)上单调递减(5分)(2)解法=由题意可得,当a>0,∈[1,2]时,(x 1)- 21≤恒成立,即当a>0,x∈[1,e2]时,“ lnx-a≤3恒成立设h(x)= |lmx-al(a>0,x∈[1,e2]),当a=2时,A(x)=-hx a(x∈(14]),则h(x)=--1<0所以h(x)单调递减h(x)=h(1)=2a≥4>,不符合题意(7分)当0 0恒成立所以函数F(x)在(0,2)上单调递增,所以e-x>1,则a 0,h(x)在[e,e2]上单调递增所以h(x)=h(e)=2-a ,令2-a 2≤,得a≥22(2-1)2(e2-1)a<2.(11分)所以32(e2-1)22(e2-1)所以综上,a的取值范围为s].(12分)解法二由题意知3-.≥0,又x∈[1,e],所以a≤3由(x 1)-2x 2≤2一得-2 ≤hx-0≤2-2x(In≤lnx-a得a≤x(In xx /(x∈[1,e2])(x 1)(In x 2 1)-x(In x a) In x x 则h(x)(x 1)2(x 1)(7分)令q(x)=lnx x (x∈[1,e2]),易知q(x)单调递增,所以q(x)≥所以h(x)>0,所以h(x)单调递增,所以A(x)m=(1)=3,所以a≤子(8分)1 p(1)=2>0,所以g'(x)>0,所以g(x)单调递增,所以g(x)m=g(e2)=所以a≥(11分)2(e2-1)22(e2-1)4,所以综上,a的取值范围为[(12分)解题关键》求解本题的关键:(1)能够对a进行合理的分类;(2)第(2)问能够根据函数解析式的特征去掉绝对值符号,进而分情况求解

21.①反而损害健康②比如饮食方面③保证充足睡眠22.(1)低温养生不能人为降温。(2)不要过多高温烹饪。(3)不要熬夜。

以上就是2022英语周报八年级外研社答案，更多英语周报答案请关注本网站。