英语周报2020—2021高三第十二期答案

221.(1)解:由题意可得………2分 =12故椭圆C的方程为4 y……………………………4分解得b=12)证明:由题意可知直线l的斜率存在且不为0,故可设直线l的方程为y=kx m(m≠0),点P,Q的坐标分别为(x,yn),(x,y)高面一0由S△N=1MOHy1,S=MO1y,S△0=51NOx1l,Sm=|NOxl化简还十= 到,J y2y 述2= J2x2-2,2)2=(ax-x22)2分yi y3即2=k27由分 y2=1,消去y得(1 4k2)x2 kmr 41)0,………………………………………8分则△=64k16(1 4k2)(1)= 1)>0,且x1 x故yy2=(kx1 m)(kx2 m)=k2x1x2 km(x1 x2) m242a2=1 因此边=81x km(x x) m2………………………10分12k2,即8k2m21 4k2 m2=011分又m≠0,所以k2=4,又结合图象可知,一一2所以直线L的斜率为定值…………12分

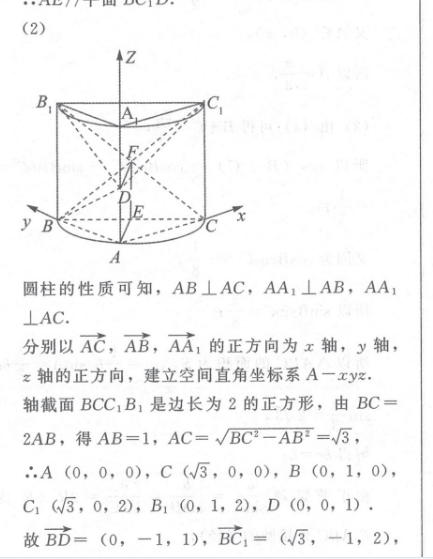
18.解:(1)存在,当点E为BC的中点时,AE//平面BC1D证明:连接B1C交BC1于点F,则点F为B1C的中点,取BC的中点E,连接AE,EF,E,F分别为BC,BC1的中点,∴EF=CC1,EF/CC1,AD-2AAl=2CC1, AD//CC1∴EF=AD,EF∥AD,∴四边形EFDA是平行四边形∴AE//DF.①∵AE￠平面BC1D,DFC平面BC1D,∴AE/平面BC1D.(2)圆柱的性质可知,AB⊥AC,AA1⊥AB,AA1⊥AC分别以AC,AB,AA1的正方向为x轴,y轴z轴的正方向,建立空间直角坐标系A-xya轴截面BCC1B1是边长为2的正方形,由BC=2AB,得AB=1,AC=√BC2-AB=√3,∴A(0,0,0),C(3,0,0),B(0,1,0),C1(3,0,2),B1(0,1,2),D(0,0,1)故BD=(0,-1,1),BC1=(3,-1,2),B1b=(0,-1,-1),设平面BC1D的法向量为n=(x,y,z),且Bdy z=0则BC1·n=√3x-y 2x=0,令z=1,则n=(√1,1)3设直线B1D与平面BC1D所成的角为0,则sin=|cos 0 1×(-1) 1×(-1)3 1 1·√0 1 1即直线B1D与平面BC1D所成角的正弦值为7

以上就是英语周报2020—2021高三第十二期答案，更多英语周报答案请关注本网站。