2021-2022英语周报高三新课程第30期答案

4.C等边三角形的高为y3,由三视图可知,该几何体的左边是一个三棱锥,右边是一个半个圆锥,由此可求得几何体的体积为83x4=-x-X4x2x23 -x-Xx22×232

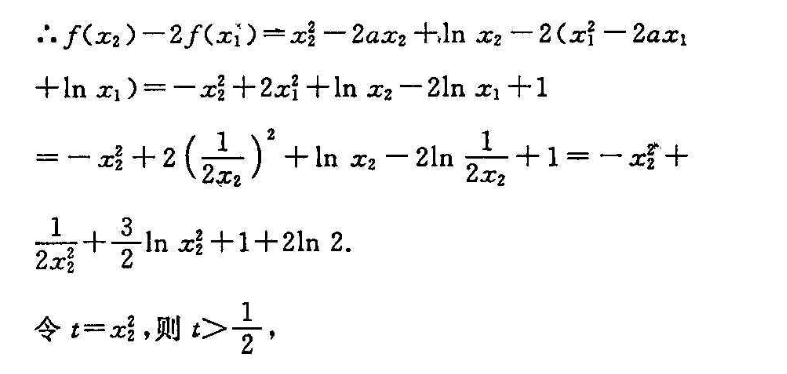
19.解:(1)由题得,(x)=2x-2a =2x2=2ax 1,x>0,令y=2x2-2ax 1,x>0,∴当△=4a2-8≤0,即一√2≤a≤√时,y≥0,此时f(x)在(0, ∞)上单调递增;当a<√时,2x2-2ax 1=0有两个负根,此时f(x)在(0, ∞)上单调递增;当a>2时,2x2-2ax 1=0有两个正根,解得x或a √a2-22此时f(x)在0,a-a2二=2)(a ∞)上单调递增在a-√a-2a上单调递减综上,当a≤v时,函数f(x)在(0, ∞)上单调递增;当《>√2时,函数f()在,22=2 )上单调递增,在(2=2a √a=2)上单调递减(5分)(2)由(1)可得,2=8一,x2a 2x1 x2=a,x1·x2=1,a>2,2ax1=2z 1,2ax2=2x2 1∴a>2,则>2”2x1∈(02),n∈(2, ∞)2,d∴f(x2)-2f(x1)=x2-2ax2 nx2-2(x-2ax1 1nx1)=-x2 2x2 lnx2-2lnx1 1=-x2 2(2) In xz-2ln.I2.1=-x2 ln2 1 21n22令t=x2,则t则g()=-t 。ln计 1 2ln2,则g(t)=-1 3==22 3t22 2t(2t-1)(t-1)当2<<1时,E(D)>0;当公>1时,g()<0,g()在(21)上单调增,在(1, ∞)上单调递减,∴g(t)mx=g(1)1 4ln22∴f(x2)-2f(x1)的最大值为1 4ln2(12分)

以上就是2021-2022英语周报高三新课程第30期答案，更多英语周报答案请关注本网站。