2022掌上周报英语听力答案

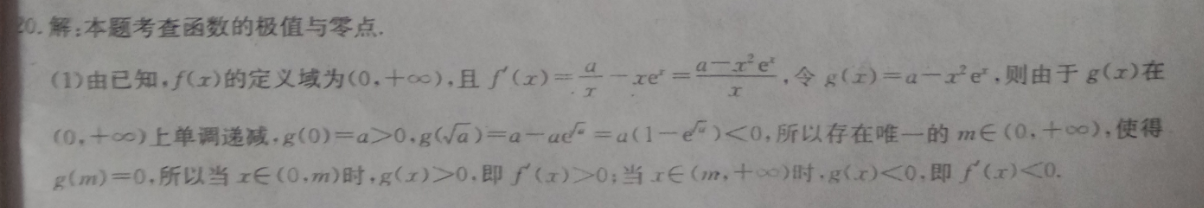
解:本题考查函数的极值与零点(1)由已知,f(x)的定义域为(0, ∞),且(x)=一x=C,令g(x)=a-xe,则由于g(x)在(0, ∞)上单调递减,g(0)=a>0,g(a)=a-ac=a(1-)<0,所以存在唯一的m∈(0, c),使得g(m)=0,所以当x∈(0,m)时,g(x)>0.即f(x)>0;当x∈(m, ∞)时,g(x)<0,即f(x)<0所以f(x)在(0, ∞)上有唯一极值点(2)因为f(2)>e(-e h2),所以a>e①由(1)知f(x)令g(x)=a-x2e,由a>e得g(1)=a-e>0,所以g(x)=0在(1, ∞)内有唯一解,从而f(x)=0在(1, ∞)内有唯一解x0,则f(x)在(1,x)上单调递增,在(x, ∞)上单调递减,所以x0是f(x)的唯一极值点令h(x)=hnx-x 1,则当x>1时,h(x)=x-1<0,故h(x)在(1, ∞)内单调递减,从而当x>1时h(x) e,lna>1时,有f(lna)=aln(lna)-(lna-1)em 1时,nx

18.解:(1)由题得x=1 2 5 4 6 5 5=4百台(1分)x=1.6 3.6 3 5 4 62=3.6百台.(2分)≈32 2 12 02 22 12 1229,s=2 02 0.62 1.4 0.4 2.42 1.624(6分(2)第一周A商品的平均利润LA=100×400=4000元(8分)B商品的平均利润LB=115×360=41400元,(10分)所以LA 5,所以第一周B商品的销量比A商品稳定,所以该电商在之后的三周应该选择B商品.(12分)

以上就是2022掌上周报英语听力答案，更多英语周报答案请关注本网站。