英语周报352021-2022答案

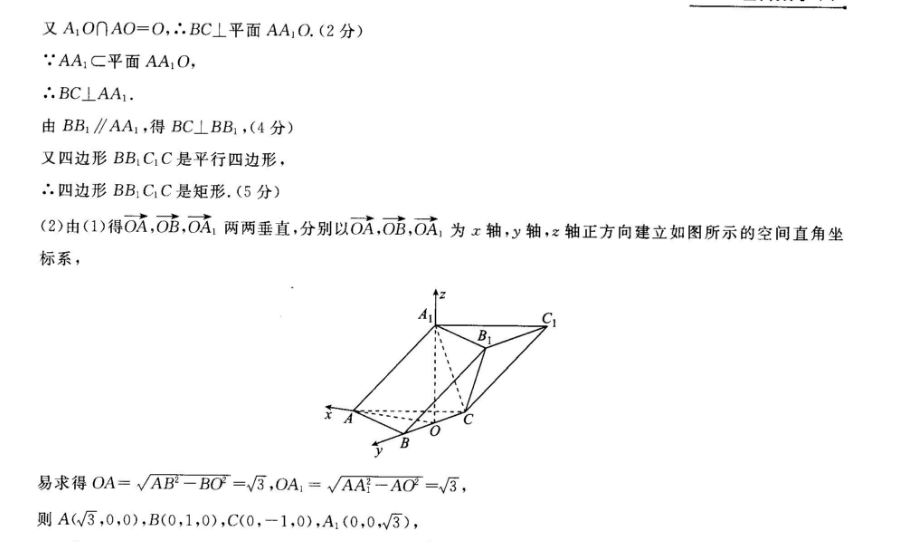
18考向预测……立体几何解答题主要考查空间中线线线面、面面位置关系的判断以及二面角(正、余弦值)的求法或点到平面的距离或几何体的体积计算等问题该部分内容每年必考,难度是中档思路……(1要证四边形BB1C1C是矩形,需证平行四边形BBC1C一组相邻的边互相垂直即可解题时充分考虑边BC的有关特征;(2)由(1)问解题基础,建立空间直角坐标系解决参考答案…1)连接AO由AB=AC,O为BC的中点,可得BC⊥AO,又∵顶点A1在底面ABC内的射影恰好为线段BC的中点∴A1O⊥BC又A1OnAO=O,∴BC⊥平面AA1O.(2分AA1C平面AA1O,∴BC⊥AA1由BB1∥AA1,得BC⊥BB1,(4分)又四边形BB1C1C是平行四边形∴四边形BB1CC是矩形.(5分)(2)由(1)得OA,OB,OA1两两垂直分别以O,O为x轴,y轴,z轴正方向建立如图所示的空间直角坐标系,易求得OA=√AB2-BO=3,OA1=√AA-AOy=√3,则A(3,0,0),B(0,1,0),C(0,-1,0),A1(0,0,3)CA1=(0,1,3),BA1=BA=(3,-1,0).(6分)设平面A1B1C的法向量为n=(x,y,z),BIA令z=1,得n=(-1,-√3,1),(9分)平面A1B1C1的一个法向量为OA1=(0,0,3),(10分)设二面角C1-A1B1-C为0,∵0为锐角∴cosb=lcos

18.【解析】(1)因为AB∥CD,AB⊥BC,AB=2CD=4,BC=√③,所以CE=DE=1所以由勾股定理得AE=√3 (=25,BE=√ y=2,所以AE BE=(23)2 2=4=AB,所以AE⊥BE,因为△PCD是等边三角形,E是CD的中点,所以PE⊥CD2分因为平面PCD⊥平面ABCD,平面PCD门平面ABCD=CD,PEC平面PCD所以PE⊥平面ABCD,所以PE⊥AE,“…又BE∩PE=E,所以AE⊥平面PBE(2)由题意得:PE⊥平面ABCD,所以PE⊥AE,PE⊥BE,5分又因为PE=3,AE=2③,BE=2,所以,PA=√(3)2 (2√3)=√1,PB=√(3) 2-、,又国为AB=4,所以∠APB=①5)= (0)=-3,则m∠pBE/05√105所以三角形APB的圆积为S△w-×√T×√72√6,根据等体积转化,V1=V,m,设点E到平面PAB的距离为d,即×5△mAXd=XS△ asX PE,20×d一×3×4X、3×5,解得d=所以点E到平面PAB的距离为

以上就是英语周报352021-2022答案，更多英语周报答案请关注本网站。