高二英语周报20182022课标答案

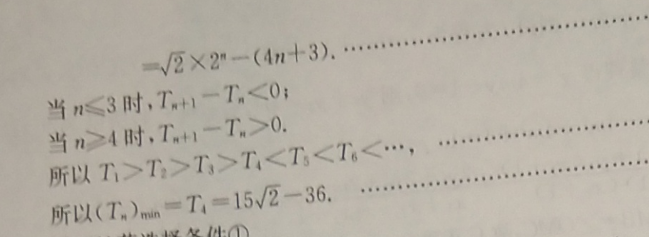
17.(1)证明:由an 1 an=2n,得an am1=2(n-1)所以an 1-an-1=2,即数列{an}的奇数项和偶数项均为公差为2的等差数列由a1=2,a2 a1=2,得a2=32分所以a1=1 (m-1)×2=2-2=(2n=1)-2a2=2 (n-1)×2=2n-23分所以an=n-14分则an 1-an=(n 1)-2所以{an}是首项为,公差为1的等差数列5分(2)解:b2-(4n-1)=y2×2-(4n-1)6分√2、2(1-2”)_n(3 4T2(2n-1)-n(2n 1)7分Tn 1-Tn=√2(2 1-1)-(n 1)(2n 3)-2(2-1) n(2n 1)=2×2"-(4n当n≤3时,T 1T所以T>T2>73>T 0.所以(Tn)mm=T4=15√2-36.………

23.(本小题满分10分)【选修4-5:不等式选讲】(1)解:当x∈[2,2时,|x 2|=x 2,所以f(x)≥4x 2恒成立,即|2x-a≥4-x-2,∴2x-a≥2-x或2x-a≤-2 x∴a≤3x-2或a≥x 2恒成立

以上就是高二英语周报20182022课标答案，更多英语周报答案请关注本网站。