2022 英语周报 高二 课标 56答案

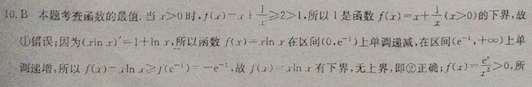
10.B本题考查函数的最值,当x>0时,1()-x1≥2>1,所以1是函数f(x)-x 1(x>0)的下界,故①错误;因为(xnx)-1 lnx,所以函数f(x)-rlnx在区间(0,e)上单调递减,在区间(e-, ∞)上单调递增,所以f(2)-nx≥(e-)--c-,故f()=xx有下界,无上界,即②正确;f(x)5>0,所以函数fx)有下界,故①错误因为≤型≤3<1,所以函数1f(x)1<,故函数f(x)有界,即④正确

18解:(1)因为函数f(x)是定义在R上的奇函数,所以f(0)=0￥x<0时,-x>0,则f(-x)=(-x)2 a(-x) 3-2a=x2…-ax 3-2a=-f(x)所以f(x)=-x2 ar-3 2a(x<0)x2 ax 3-2a,x>0所以f(x)={0.x=0(6分)x2 ax-3 2a,x<0(2)若f(x)是R上的单调函数,且f(0)=0,则实数a满足!23-2a≥0解得0≤a≤故实数a的取值范围是0(12分)

以上就是2022 英语周报 高二 课标 56答案，更多英语周报答案请关注本网站。