英语周报2021-2022高二27期答案

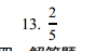
13.5

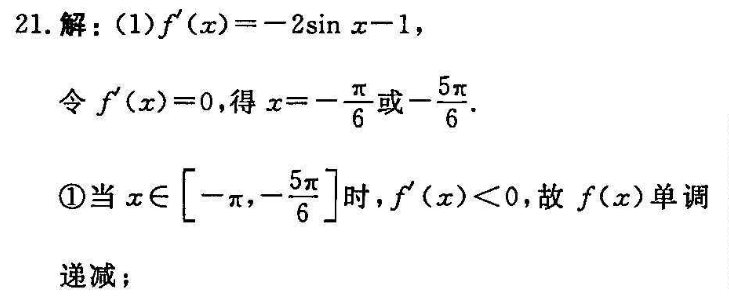
21.解:(1)f(x)=-2sinx-1,令∫(x)=0,得x=-7或一5①当x∈丌,-5时,∫(x)<0,故∫(x)单调递减;当x∈[一5,一否]时,r(x)>0,f(x)单调递增,且f(x3>0,6所以f(x)在区间|-r,上没有零点.(3分)②当x∈-4,x时,f(x)<0,故f(x)单调递减,又f(-)=3 百>0,()=-2-x<0,f(-)·f(n)<0所以函数f(x)在r上存在唯一的零点综上所述,f(x)在[一,]上存在唯一的零点(6分)(2若存在xe(2),使得不等式f(x) ax>2邮存在∈(0,2),使2 ax-x-2>0成立it g(r)=f(r)tax-2=2cos xtax-x-2则g(0)=0,g(x)=a-1-2sinx,当x∈(’2)时,1 2sinx∈(1,3),所以g(x)∈a-3,a-1),由于a-1≤0,即a≤1时,g(x)<0,g(x)单调递减,g(x) 0,即a>1,此时g(0)=a-1>0,因为()=a-1-2mx在(0,受)上单调递减,当a-3≥0时,g(x)>0,所以g(2)在(0,2)上单调递增,g()>g(0)=0,即f(x) ax>2;当a-3<0时,总存在∈(O,2),使得g()=0,所以存在区间(0,t),使x∈(0,t)时,g(x)>0,所以g(x)在(0,t)上单调递增,则当x∈(0,t)时,g(x)>g(0)=0,即f(x) ax>2,所以实数a的取值范围是(1, ∞)(12分)

以上就是英语周报2021-2022高二27期答案，更多英语周报答案请关注本网站。