英语周报2018-2022高中答案

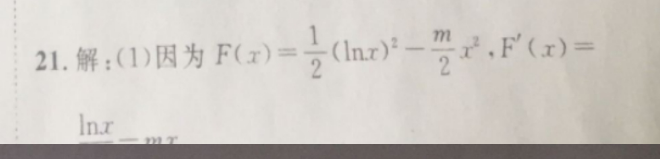
21.解:(1)因为F(x)=(lnx)2r, F(r)①若F(x)在其定义域内单调递增,则F(x)=xmx≥0在(0, ∞)恒成立,即—≥m恒成立令f(x)=hnr则了1-2l,当x∈(0、G)时,广(x)>0,f(x)单调递增,当(C, ∞)时f(x)<0,f(x)单调递减,所以f(x)在(0, ∞)无最小值,此种情况不成立,②若F(x)在其定义域内单调递减,则F(x)=Inrmx≤0在(0, ∞)恒成立,即一≤m恒成立,由①可知f(x)-=f(、0)=,所以m≥综上,若函数F(x)在其定义域内是单调函数,则实数m4分(2)若F(x)有两个极值点x1,x,则x1,x为F(x)=mx=0的两个根,即的两个根,由(1)可知,0 2m,先证x1·x>e,即证lnx1 lnn2>1,由lnn=mx12,lnx2=mx2得Inn, Inn, m(,' r,'). Inr-Inr,am(rx2),两式相除得Inn, Inr, a1 x( InInr.)) 13)-季()=,·x>0,x2>0=,则即证·m5>1,即证ln< 1其中0<1<12(t-1)令(1)=lm--千10则h'(n)=1)t(x 所以k(1)在0<<1时单调递增,所以h((12分)h(1)=0,即证,

20.【解析】(1)依题意得:4 y2=1设P(x1,y),Q(x,y),线段P考p9(2)设直线PQ的方程为y=k(x-3),k≠0,将y=k(x-3)代入 y2=1,得(1 4k2)x2-83k2xBP N(A 36144)8分)∠TPQ=∠QP,;直线TN为线段PQ的垂直平分线TN⊥PQ,则kN·k=-1,即4√3k2(10分)当k>0时,4k 1≥4,所以!∈(0当k<0时,4k ≤-4,所以t∈综上在点,使得∠7PQ∠Q,且的取值花国为[3,0)U(3(12分)

以上就是英语周报2018-2022高中答案，更多英语周报答案请关注本网站。