


(1)f(x)=-ax-2.定义域Rf(r)=e-a.①a≤0时,广(x)>恒成立,则f(x)在R上单调递增②a>0时,由f(x)=0得x=lna.x∈(-∞,lna)时,f(x)<0,f(x)单调递减x∈(lna, ∞)时,厂(x)>0,f(x)单调递增综上当a>0时,f(x)的单调递减区间为(一∞0lna),单调递增区间为(lna, ∞)当a≤0时,f(x)在R上单调递增4分(2)(x) 1=c-x=1令h(x)=e2-x-1,x>0h(x)=c-1>0恒成立h(x)在(0, ∞)上单调递增∴h(x)>h(0)=0f(x) 1>0不等式|(x) 1

9.(1)证明:∵底面ABCD为正方形,平面MAD⊥平面ABCD,平面MAD∩平面ABCD=AD,又∵CD⊥AD,∴CD⊥平面MAD,∵AMC平面MAD,∴CD⊥AM,∵MA⊥MD,MD∩CD=D,∴AM⊥平面MDC,∵AMC平面MAB,∴平面MAB⊥平面MDC.………6分(2)因为MA=AD=1,MA⊥MD,则AD=√2因为平面MAD⊥平面ABCD,所以点M到平面ABCD的距离为立AD=210分几何体 AMDCNB的体积V=2V四棱锥M-ABCD=2×()2×2=2……12分

以上就是2022七年级英语周报40期答案,更多英语周报答案请关注本网站。

 相关文章
相关文章


 栏目最新
栏目最新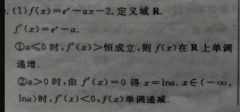

 随机推荐
随机推荐 热门标签
热门标签