2022-2022数学周报高二课标答案

22.解:(1)将直线l的参数方程消去参数t,可得直线l的普通方程为2x y-10=0.将p2=x2 y2,Cos0=x代入曲线C的极坐标方程,可得曲线C的直角坐标方程为9x2 4y2=36,即 故曲线C的参数方程为2cosy=3mPp为参数)(2)设M(2cosg,3sing),则M到l的距离d4cos c 3sin -10-10-5sin( r)√5其中tanr=3当sin(g r)=1时,d取得最小值5故|MN的最小值为√5

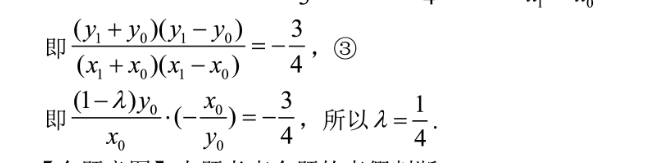
16.【答案】【命题意图】本题考查椭圆的综合应用【解析】设A(x0,y),Qx1,y,M(x,y),则B(-x,-y),P(x0,-y),x设AM=AAP,则(xM-x0,yM-y0)=(0,-2y0),所以yM=(1-24)y由AB⊥AQ,则yo yI-yo再由B,M,Q三点共线,多当 (-y,②x又因为x 20yI所以两式相减可得:=y02x2-x2即44即(y y0)(1-y)3(x x)(x-)4’③(1-d)yox即3所以元4

以上就是2022-2022数学周报高二课标答案，更多英语周报答案请关注本网站。