数学周报八年级2022-2022北师大10期答案

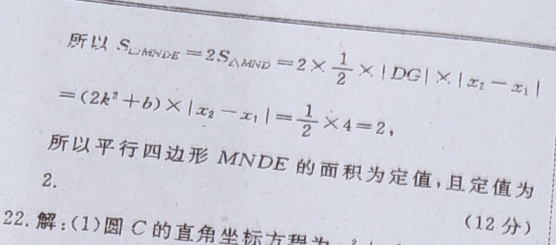
21.解:(1)设准线与y轴的交点为点H,连接QF,PF,因为△PQF是正三角形所以|PF|=|QF|=|PQ|=8(2分)在△QFH中,∠QHF=90°,∠FQH=30所以|HF=2/QF|=p=4所以抛物线C的方程为x2=8y.(5分)(2)由题意知,直线MN的斜率存在,设其方程为y=kx b,M(x1,y1),N(x2,y2),y=kr由整理得x2-8kx-86=0,△=2k2 b0则x1 x:=8k,x1x2=-80所以y y2=k(x1 x2) 2b=8k2 2b,设MN的中点为G,则点G的坐标为(4k,4k2 b),(7分由条件设切线的方程为y=kx t,ry=kItt,则由整理得x2-8bx-8t=0,1=83因为直线与抛物线相切,所以△=64k2 32t=0,所以t=-2k2,所以△=642 32t=0,所以t=-2k2,所以x2-8x 16k2=0,所以x=4k,所以y=2k2,所以切点D的坐标为(4k,2k2),(9分)所以DG⊥x轴,所以|DG|=2k2 b,因为|x2-x1=4,又因为(2-x1)2=(x2 x1)2-4x1x2=64是 32b,所以22 b=所以SM=2SA=2X2×|DG|×|x2-x1(2k2 b)×1x-x1=3×4=2所以平行四边形MNDE的面积为定值,且定值为2.解:(1)圆C的直角坐帮(12分)

11.D解析】f OCOSnxxI-Isin而n2x1的图象如图所示元2由图可知,函数y=|sn2x|的最小正周期T=,故函数f(x)的最小正周期T=2,故①错误;函数y=1s12在(,)上为减面数,则函数y=1sin2x在(x,)上为增函数,故函数f(x)在(,2)上单调递增,故②正确;:(x)的图象的对称轴为直线xk4(∈2,故③错误;由0≤lsin2x|≤1,得函数f(x)的值域为[0,1]故④正确.故选D

以上就是数学周报八年级2022-2022北师大10期答案，更多英语周报答案请关注本网站。