英语周报高一课标2021-2022第33期答案

21.【解析】(1)由f(x)=e-1-x,得f(x)=e-1-1,令f(x)=0,得x=1.…2分当x∈（一o∞，1）时，f(x)<0,f(.x)单调递减，当x∈(1， ∞)时，f(x)>0,f(x)单调递增，故f(x)在x=1处取得极小值，即为最小值f(1)=0,故f(x)≥0对于Hx∈R恒成立.……4分(2)方法一：由f四≥a(x-1-lnx),得e1-h-1≥a(x-1-lnx）.…5分设g(x)=x-1-lnx(x>0),g'(x)=1-1,令g'(x)=0,得.x=1.当x∈(0,1)时，g'(x)<0,g(x)单调递减，当x∈(1， ∞)时，g'(x)>0,g(x)单调递增，故g(x)在x=1处取得极小值，即为最小值g(1)=0,即e-l≥at对Ht∈[0， o∞)恒成立，….7分设h(x)=e-ax-1(.x≥0)，h'(x)=e-a,当a≤1时，h'(x)=e一a≥0，即h(x)在[0， o∞)上单调递增，而h(0)=0,则h(x)≥0恒成立.…9分当a>1时，令h'(x)=e-a=0,得x=lna,当x∈(0，lna)时，h'(x)<0,h(x)单调递减，而h(0)=0,故x∈(0，lna)时，h(x)<0,即h(x)≥0不恒成立.11分综上，a的取值范围为（一∞，1].…12分(2)方法二：由f2≥a(x-1-nx)得-1≥a(x-1-lnx）等价于e二-1-a(x-1-lnx)≥0，设g(x)=-1-a(x-1-1n),且g1)=0,则g）=》-a2(e1-ax.…5分2则当a≤1时，由x∈(0，十o∞)，e-1-a.x≥e-1一x,由(1)得，e-1-x≥0，即e-1-a.x≥0，…7分所以r∈(0.1)时，g(x)=宁(e1-ar)<0,g(x)单调递减，x∈(1，十∞)时，g(x)=(e1-ax)>0,gx)单调递增，故g(x)在(0， ∞)上的最小值为g(1)=0,即f(x)一a(x2一x一xlnx)≥0恒成立.……9分而当a>1时，设h(x)=e-1-ax,x∈(0，十∞)，令h'(x)=e-1-a=0,得x=1 lna,由a>1,故x=1 lna>1.当x∈(1,1 lna)时，h'(x)<0,h(x)单调递减，故xe1,1 lna时gx)=(e1-ar)=h)<0,则g(x)单调递减，而g(1)=0,即x∈(1,1十lna)时，g(x)<0,故f(x)-a(x2-x-xlnx)≥0不成立，……11分综上，a的取值范围为（一∞，1].12分

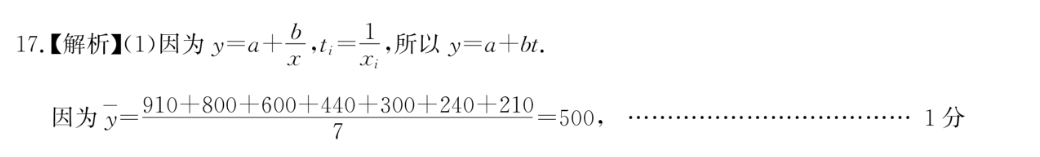
17.【解析11)因为y=a十4，=己，所以y=a十u.因为y=910 800 600 440 300 240 210=500,·…1分7∑ty:-7y所以b=i=1750-7×0.37×5004559100…3分∑号-70.550.5511i=所以a=y-bt=500-2×0.37-2.所以y23 9402.…5分1111所以所求回归方程为y=2133,91001111x6分(2)随机变量X的可能取值为3,4,5，…............7分P(X=3)=(号)' (3)广=3，P(X=)-Cc(号)}×号×号 c(号)×号×3-27PX=)=C(号)×(3)×号 C(3)》×(号)×3-…10分X345所以随机变量X的分布列为11分P32号27EX)=3×号 4×29 5×1072712分

以上就是英语周报高一课标2021-2022第33期答案，更多英语周报答案请关注本网站。