
15.>S6>S1






解:(1)由题意,不妨设Ω(x,y),则P(4,y),OP=(-4y),OQ=(x,y),O在以PQ为直径的圆上,OP00-0(-4,y)·(x,y=-4x y2=0,曲线C的方程为y2=4x(2)(法一)设A(xy),B(x2,y2),D(x3,y3),M(m,0),N(n0)依题意,可设:x=0 a(其中a=2),……=ty a,由方程组消去x并整理,得则y y2=4,Hy2=-4a=-8,分同理,yy=-4m…8分又∵AD=3AM,(x-x,y3-)=3(m-x1,-y),3-y=-3y1,y2Hm一1=上一y2B1NH2=x21x1-y2=2 y)-4y2=8F2 2当t=0时,△BMN面积取得最小值,其最小值为8212分(2)(法二)设直线1:x=my 2,A(x,y1),B(x2,y2),Dx3y)由方程组y2=4x,消去x并整理,得y2-4my-8=0则y1y2=-85分AD=3AM,由法一,可知y3=-2yy2y3=16,y1y设laD:x=my b由方程组{x= b消去x并整理,得y2-4-4=0则b=-4,即N(-40)设l0:x=sy t同理,可得y= 4=-1238即M(2,0),MNF- 40分 2|y282(当且仅当y2上22时,等号成立)△BMN面积的最小值为8互分3AM,由法一,可知y=-2yy2y3=16而k=当。4x,-Y V, y3同理,lm:y-y2=(x-2),令y=0,则x=、2=-4IMNF4 2SB=IMNI-I3, =5(4 1)2y1||y(当且仅当|y1=22时,等号成立)△BMN面积的最小值为8212分(法四)令AE=1EB(>0),则2-x=1(x2-2),由法一,可知yy2=-8,=10D)=4,由方程组2-x=1(2-可解得x=2,x2=,xx,=4根据抛物线的对称性,不妨令点A在第一象限,即y>0,y2<0,2),B(6分又∵:AD=3AM,由法一,可知y=-2y1,y2y3=16,D(8,-4),M(40),b设la0:x=m b,由方程组y2=4x,消去x并整理,得y2-4my-4b=0,则-4b=16b=-4,即N(40)IMNF4 410分MNy2上4( )28(当且仅当=1时,等号成立),△BMN面积的最小值为8E【命题意图】本题以直线与抛物线为载体,其几何关系的向量表达为背景,利用方程思想韦达定理构建目标函数,利用坐标法解决几何问题贯穿始终,主要考查直线与抛物线的位置关系及定点问题、最值问题,考查学生的逻辑推理,数学运算等数学核心素养及思辨能力

以上就是数学周报2022-2022第3期答案,更多英语周报答案请关注本网站。

 相关文章
相关文章



 栏目最新
栏目最新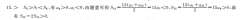

 随机推荐
随机推荐 热门标签
热门标签