
9.C【解析】“平民和贵族展开了长达两个世纪的斗争”说明平民和贵族之间有矛盾,结合所学可知,在罗马共和国时期,一开始贵族是享有很多特权的,而平民没有,所以平民就为了追求平等的权利而斗争,斗争的结果是通过颁布一系列法律达到“氏族贵族和平民不久便完全溶化在国家中了”,也就是说在法律上最终确定了双方平等的地位,故选C项:“贵族的特权被取消”本身说法错误,A项排除;罗马法体系最终形成的标志是6世纪东罗马帝国皇帝查土丁尼组织编写的《民法大全》,而题干讲的是在罗马共和国时期,故B项与题干时间不符,所以排除;自由民不仅仅包括罗马公民,而共和国时期的罗马法只适用于罗马公民,故D项不符合题意,排除。
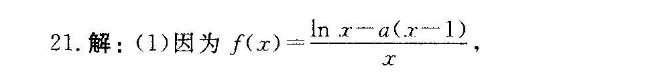


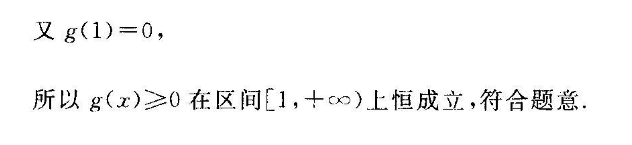

21.解:(1)因为f(x)In x-a(2-1)所以函数f(x)的定义域为(0, ∞),且f(r)(2分)令f(x)>0得lnx<1解得0 1-a,解得x>e-a所以函数f(x)的单调递增区间为(0,c1“),单调递减区间为(el-, ∞)(5分)(2)当x≥1时,1-xf(x)≤e-等价于e-1 lnx& g(x)=e In x-ar a-1=e In x-a.x 则g(x)=e-1 1-a,(7分设h(x)=g(x),则h(x)=et8分)因为当x≥1时,h(x)>0所以h(x)在区间[1, ∞)上单调递增,即g'(x)在区间[1, ∞)上单调递增因此,g'(x)mn=g'(1)=2-a,(9分)当a≤2时,g(1)≥0,g(x)≥0在区间[1, ∞)上恒成立,所以g(x)在区间[1, ∞)上单调递增.又g(1)=0所以g(x)≥0在区间[1, c)上恒成立,符合题意当a>2时,g(1)<0,存在x∈(1, ∞),使得当x∈(1,x)时,g(x)<0,从而g(x)在区间[1,x。1上单调递减,又因为g(1)=0所以当r∈(1.xn)时,g(x)<0,不合题意综上,a的取值范围为(-cx,2](12分)

以上就是2022 英语周报 高三高中英语总复习hz答案,更多英语周报答案请关注本网站。

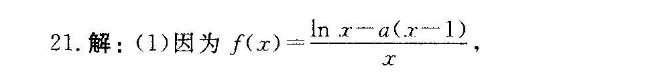


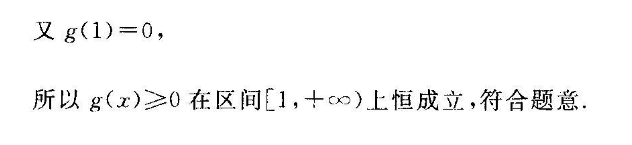



 相关文章
相关文章


 栏目最新
栏目最新

 随机推荐
随机推荐 热门标签
热门标签