2022 英语周报 八年级 牛津 2答案

解:(1)因为以点P为圆心,以|PF为半径的圆过原点O所以1PO|=1PF,设线段OF的中点为E,则PE⊥OF,所以a=,(2分)因为点P(4,22)在抛物线C上,所以8=2×2,p=4,(4分)所以抛物线C的方程为y2=8x.(5分)(2)设A(x1,%1),B(x2,y2),直线l的方程为x=my n,联立y2=8x得,y2-8my-8n=0,△=(8m)2 4×8n>0,得2m2 n>0,所以y1 y2=8m,yy2=-8n,(7分)因为RA⊥RB,所以成,商=(x1-2,y-4)·(x2-2,y2-4)=(x1-2)(x2-2) (y1-4)(y2-4)=2)82) (y1-4)(y2-4)=(y1-4)(y2-4)[(y 4)(y2 4) 1]=0,因为点R与点A,B不重合,所以(y1-4)(y2-4)≠0,所以 4)(2 4) 1=0,整理得yy2 4(y1 y2) 80=0,即-8n 32m 80=0,所以n=4m 10,(10分)尺(29)代入x=my n得x=m(y 4) 10所以直线l经过定点Q(10,-4),(11分)0-2)2 (-4-4)2=82,所以当RQ⊥l时,点R到直线l距离的最大值为82.(12分)

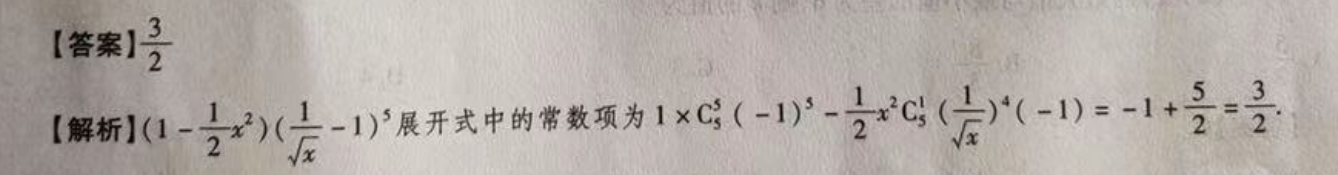
【答案】【解析1(1-1x2)(11)展开式中的常数项为1×(-1)、与2G)(-1)=-1 5=3222

以上就是2022 英语周报 八年级 牛津 2答案，更多英语周报答案请关注本网站。