英语周报高二课标版2021-2022答案

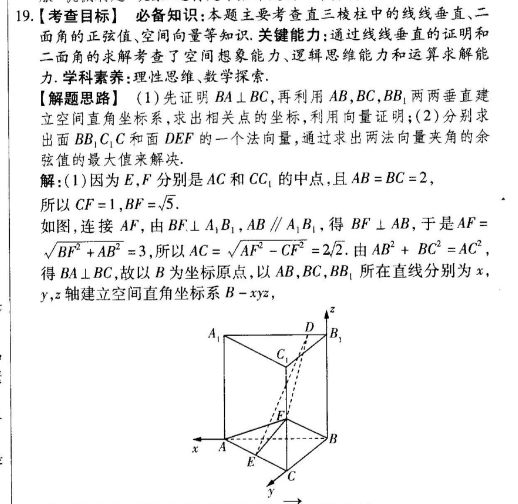
19.【考查目标】必备知识:本题主要考查直三棱柱中的线线垂直、二面角的正弦值、空间向量等知识.关键能力:通过线线垂直的证明和二面角的求解考查了空间想象能力、逻辑思维能力和运算求解能力学科素养:理性思维、数学探索【解题思路】(1)先证明BA⊥BC,再利用AB,BC,BB1两两垂直建立空间直角坐标系,求出相关点的坐标,利用向量证明;(2)分别求出面BB1C1C和面DEF的一个法向量,通过求出两法向量夹角的余弦值的最大值来解决解:(1)因为E,F分别是AC和C1的中点,且AB=BC=2所以CF=1,BF=√5.如图,连接AF,由BF⊥A1B1,AB∥AB,得BF⊥AB,于是AF=BF ABF=3,所以AC=√AF-CF=2.由AB2 BC2=AC2,得BA⊥BC,故以B为坐标原点,以AB,BC,B1所在直线分别为x,y,z轴建立空间直角坐标系B-xy则B(0,0,0),E(1,1,0),F(0,2,1),BF=(0,2,1)设B1D=m(0≤m≤2),则D(m,0,2),于是DE=(1-m,1,-2)所以B.DE=0,所以BF⊥DE(2)易知面BB1C1C的一个法向量为n1=(1,0,0)设面DFE的法向量为n2=(x,y,2),n,又靂=(1-m,1,-2),E=(-1,1,1)所以(1-m)x y-2z=0-x y z=0,令x=3,得y=m 1,z=2-m,于是,面DFE的一个法向量为n2=(3,m 1,2-m),所以cos(n1,n2〉=)2设面BCC与面DFE所成的二面角为6,则in6=√1-m(n1,m2),故当m=时,面BBCC与面DFE所成的二面角的正弦值最小为,即当B1D=时,面BB1C1C与面DFE所成的二面角的正弦值最小.【解題关键】本题求解关键是建立恰当的空间直角坐标系,确定相关点的坐标,再利用空间向量进行运算

13.(1)C(2分)(2)C(3分)(3)0.855(3分)【解析】(1)本实验采取的研究方法为控制变量法,C项正确。(2)在平衡摩擦力后,用砝码桶与砝码的总重力代替绳子的拉力,前提条件是砝码桶与砝码的总质量远小于小车的总质量,随着砝码桶与砝码的总重力增大,装置的加速度增大,绳子的拉力将小于砝码桶与砝码的总重力,使得小车实际加速度将小于理论加速度(虚线所示),图象向下弯曲。故aF图象接近图2中的C图。(3)相邻两计数点间的时间间隔T=5×0.02s=0.1s,由还差法可得(3 s4)-(s1 s2)=a(2T)解得a=0.855m/s2。

以上就是英语周报高二课标版2021-2022答案，更多英语周报答案请关注本网站。