

22.解:由题得,f(x)= Sin acos √3oCos X√3e sin 2x o cos 2x=sin ( 2x T(2分)()x∈(0,2),可得2x 3∈(,纡),则sn(2x 3)∈(-2所以函数y=f(x)的值域为(2(4分)(2)若f(a)=t,即sm(2a 3)=1,因为a∈(,2)所以2a ∈(,又sin(2a )∈(0,),所以2a ∈(,x)6分)所以(2 3)=√-(2 3)(8分)所以c2=(2 )-3](a 2)∞3 s1(2 3)=m=2s(12分)


22.【解题思路】(1)消去参数6,将曲线C的参数方程化为普通方程,利用pcos6=x,psin6=y,将直线l的极坐标方程转化为直角坐标方程;(2)设曲线C上一点P(3cos6,3sin),利用点到直线的距离公式、辅助角公式,结合三角函数的有界性求解x=3cos e解:(1)由(θ为参数)消去参数y=3sin 6得曲线C的普通方程为x2 y2=9.(3分)将 pcos 6=x,psin=y代人3 pcos 8-2psin06=0,得直线l的直角坐标方程为3x-2y-6=0.(5分)(2)设曲线C上一点P(3cos6,3sin0)到直线l的距离为d,则d=13×3c0s0-2×3sin6-6132 (-2)19c0s 0-6sin 6-6313cos(0 g)-61(tan13当(c( 9)=1时,。3,(9分)=3 13613(10分)

以上就是2022-2022年数学周报八年级上册人教版第3期答案,更多英语周报答案请关注本网站。

 相关文章
相关文章



 栏目最新
栏目最新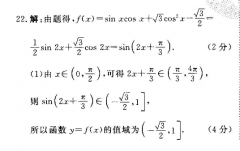

 随机推荐
随机推荐 热门标签
热门标签