

20.【解析】(1)由题意,令 2hrs3.t< 2kπ(k∈Z),2 2kn53x5 2km(k∈Z),则一4 4k5x52 4kr(k∈Z),3取k=0,得-≤x≤,取k=1,得=≤x≤故函数f(x)在[0.x]上的单调递增区间为[0.-π].(4分)(2)当xe[0,时,3x ze[2,5,列表如下66933L(x)20√3根据表格,作出函数f(x)在[0,m上的大致图象如下:(8分)(3)将函数()的图象向右平移个单位长度,得到y=25m(3(x-) 巧=2sin(3x-的图象,再将横坐标伸长为原来的2倍(纵坐标不变)得到8)=smnx-)的图象当x∈x2n]时,32个33故当xk(x)取得最大值2.(12分)432




21.解:(1)题得,f(x)的定义域为(0, ∞),f(x)=(=1)(a-1)x(1分)当a≥1时,f(x)>0,函数f(x)在(0, ∞)上单调递增;(2分当a<1时,记g(x)=1 (a-1)x,则函数g(x)=1 (a-1)x在(0, ∞)上单调递减,令g(x)=0→x=1所以当x∈(0,1)时g(x)>0,即f(2>0,函数f(2)在(O,12)上单调递增当x∈(1, ∞)时g()<0,即f(x)<0,函数f(x)在(1, ∞)单调递减(5分)综上可知:当a≥1时,函数f(x)在(0, ∞)上单调递增;当a<1时,函数f(x)在(f-a)单调递增,在(12, ∞)上单调递减,(6分)2)当a=0时,(x)=lmx-x 1,/(x)=1-1一由)可知,函数∫(x)在(0,1)上单调递增,在(1,∞)上单调递减,所以x=1为函数f(x)的极大值点,所以f(x)≤f(1)=0(8分)因为g(x)=2x2-4x m=2(x-1)2 m-2,所以g(x)≥m-2,当且仅当x=1时,g(x)m=m-2.(10分)所以m-2≥0→m≥2,所以m的最小值为2.(12分)

以上就是2022 英语周报 八年级 新目标KMD 6答案,更多英语周报答案请关注本网站。

 相关文章
相关文章



 栏目最新
栏目最新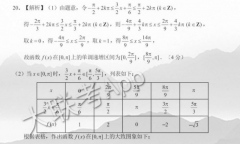

 随机推荐
随机推荐 热门标签
热门标签