

21.(1)解:f(x)=ae-sinx,f(0)×(-1)=-a=-1,则a=1.1分当x≤0时,0 0时,e>1,1≤sinx≤1,f(x)=e-sinx>0所以f(x)在(0, ∞)上单调递增4444.4444...4443分因为f(0)<0,f(2)>04分所以f(x)在(0, ∞)上存在唯一的零点5分综上,f(x)的零点的个数为1.……6分(2)证明:设函数g(x)=f(x)-(x-1)=e-x cosx-2(x>0),则g'(x)=e-1-sinx,设h(x)=g(x),则h'(x)=e-cosx.7分因为x>0,所以e>1,-1≤cosx≤1,所以h'(x)>0,8分则h(x)在(0, ∞)上单调递增,则h(x)>h(0)=0,………………………………………9分即g'(x)>0,从而g(x)在(0, ∞)上单调递增,…10分于是g(x)>g(0)=0,11分故f(x)-(x-1)>0,即f(x)>x-1对x∈(0, ∞)恒成立…12分评分细则:【1】第(1)问的解析的第3行未写e>1,-1≤sinx≤1,而直接得出f(x)>0,则扣1分.第5行只要得到一个函数值小于零,一个函数值大于零,即可得分【2】第(2)问的解析的第3行若未写e>1,-1≤cosx≤1,而直接得出h'(x)>0,则扣1分

11.D【解析】本题考查椭圆定义的应用,考查数形结合的数学思想依题意可设椭圆C的方程为2 =1(a>b>0,连接AF2,如图所示由题意,AF1|=3F1B|,则AB|=4|F1B|,又4|BF2|=5AB|=20|F1B|,得BF1=5F1B|,由椭圆定义得|BF1 |BF2|=6FB|=2a,则F1B|=3a,所以AF=a, t AF2=2a-lAF=a

以上就是数学周报 2020~2021七年级 第七期答案,更多英语周报答案请关注本网站。





 相关文章
相关文章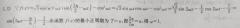
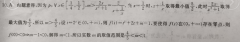

 栏目最新
栏目最新

 随机推荐
随机推荐 热门标签
热门标签